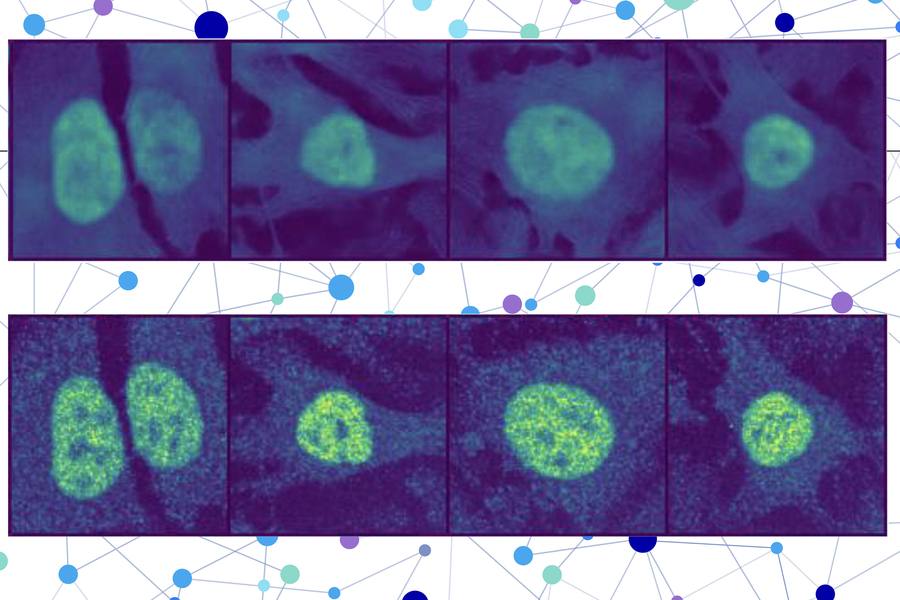
World’s Biodiversity & Ecosystem
Highlights
Artificial Intelligence
SPACE AND ASTROPHYSICS

Meteorological satellites observe temperatures on Venus
Imaging data from Japan’s Himawari-8 and -9 meteorological satellites have been successfully used to monitor temporal changes in Venus’ cloud-top…
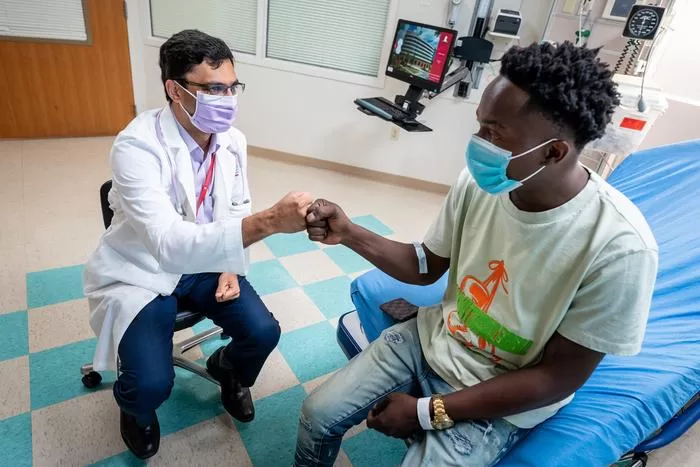
HEALTH
SOCIETY
Culture | Policy | Education | Economics | Entertainment